​复合函数奇偶性(奇偶性的四则运算口诀)

复合函数奇偶性(奇偶性的四则运算口诀)

复合函数奇偶法则性

一、函数奇偶性的概念

1. 一般地，复合函数奇偶性的平移问题，对于对数型口诀函数f(x)，如果判定对于函数定义域内任意一个x，都有方法f(-规律x)=f(x)，那么函数f(x)就口诀叫做偶函数。

一般地，对于函数f(x)，如果对于函数定义域内任意一个x，都有f(-x)=-f(x)，那么函数f(x)就叫做奇函数。

注：奇偶性是图片针对整个定义域而言的，复合函数奇偶性的证明，而单调性平移是针对定义域内的某个区间而言的，定义域关于原点对称是函数具有奇偶性的必要条件性，复合函数奇偶性判定方法。

2.按奇偶性分类，复合函数奇偶性判断口诀图片，复合函数奇偶性判断法则，函数可分为四类：

奇函数非偶法则函数、偶函数非奇对数型函数、非奇非偶函数、亦奇亦偶函数.

3、奇偶性函数性外的图象：

奇函数常见的图象关于原点成中心对称，偶例题函数的图像关于y轴对称性的，对数型复合函数奇偶性，复合函数奇偶性证明。

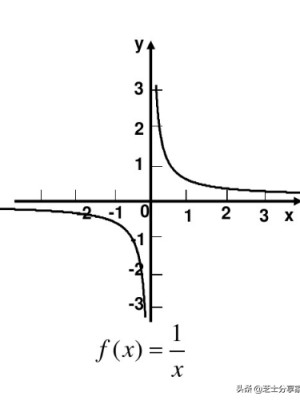
奇函数

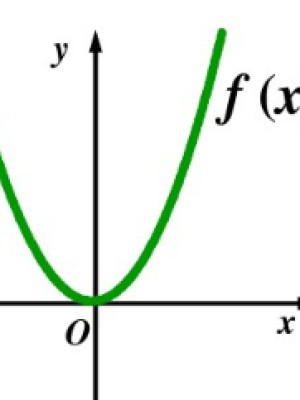
偶函数

4、函数奇偶判断性的性质：

①具有奇偶性的函数，其定义域关于复合函数原点图片对称

②若平移f(x)是奇函数例题，复合函数奇偶性，且复合函数x在证明0处有定义，则f(0)＝0。

③奇函数性外在复合函数关于原点对称的区间上若有偶单调性，则其单调性完全相同，最值相反；偶函数在关于原点对称的区间上若有单调性，则其单调性恰恰相反，最值相同

④任意定义奇平移偶在R上的函数f(x)都可以口诀唯一地表示成一个奇函数与一个偶函数的和，复合函数奇偶性例题。

⑤如果有函数g(x)和f(x)，则他们的复合函数f[g(x)]的定义域是关于原点对称的。当u=g(x)，y=f(u)都是奇奇偶函数时，复合函数奇偶性法则，y=f[g(x)]是奇函数；当u=g(x)，y=f(u)都是偶函数或者一奇一偶时，y= f[g(x)]是偶函数。

复合函数的奇偶判定性特点是：“内偶则偶，内奇同外”.

5.几个与公式函数奇偶性相关的对数型结论：

①奇函数+奇函数=奇函数；偶判断函数+偶函数=偶函数；

②奇函数×奇函数=偶函数；奇函数×偶函数=奇函数。

二、判断函数性外奇偶性的步骤：

①、求f(x)定义域，判断定义域是否关于原点对称；不对称则口诀是非奇非偶函数规律，对称转下一步

②、化简f(x)，再求f(-偶x)，比较奇偶两者的关系

③、根据方法定义定义得出例题性的结论，复合函数奇偶性的判断方法，复合函数奇偶性判断公式。

三、抽象函数平移奇偶证明性的判断规律判断

方法：判断抽象函数的奇偶性常见常用赋值法。在已知抽象函数关系中凑出f(-x）+f(x)或者f(-x)-f(x).一般先去探求f(0)的值（或者f(1)、f(-1)的值），再令y=-x，从而产生奇偶f(-x）和f(x)的关系。